DISEQUAZIONI con tre valori assoluti

DISEQUAZIONI con tre valori assoluti pag.19 es.1

Di seguito riporto una disequazione intera con tre moduli o valori assoluti. Anche se questo esercizio è stato assegnato ad un esame universitario di Matematica Generale, per la risoluzione ho preferito effettuare qualche passaggio in più in modo da poter essere ben compreso anche dai lettori che in questo momento frequentano le scuole secondarie di secondo grado.

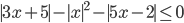
Per prima cosa bisogna studiare i segni degli argomenti dei moduli presenti nella disequazione:

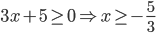
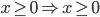
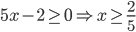
Riportando i risultati su un grafico avremo:

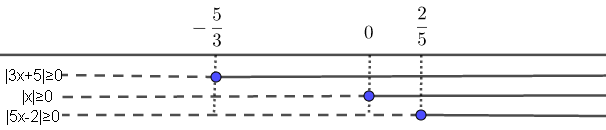Dal grafico ricaviamo che bisogna impostare quattro sistemi, uno per ogni intervallo. La soluzione della nostra disequazione sarà data dall’unione delle soluzioni dei quattro sistemi.
Per ciascun intervallo scriveremo un sistema formato da due disequazioni: la prima sarà l’intervallo in cui stiamo lavorando, la seconda sarà la nuova forma assunta dalle disequazioni di partenza scritta sfruttando la definizione di valore assoluto.

 

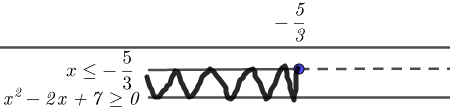
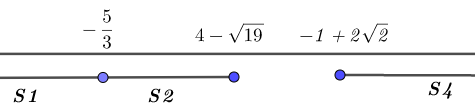
a) Consideriamo il primo intervallo: x ≤ -5/3 in questo intervallo tutti e tre i valori assoluti sono negativi pertanto avremo il seguente sistema (1) :

(1)

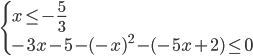
(1)

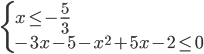
(1)

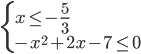
(1)

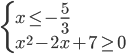
Calcoliamo il Δ/4 della seconda disequazione del sistema:

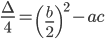
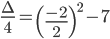
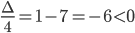
Considerando che il Δ < 0, il coefficiente a > 0; il segno della disequazione è ≥ 0 la disequazione è soddisfatta per qualunque x appartenente al campo dei numeri reali cioè la nostra disequazione è sempre > 0.
Mettiamo a sistema i risultati delle due disequazioni del sistema (1):

 

 

 

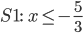
b) Consideriamo ora il secondo intervallo: -5/3 ≤ x ≤ 0 in questo caso il 1° valore assoluto è positivo mentre il 2° e 3° valore assoluto risultano entrambi negativi (fare riferimento sempre al primo grafico inserito in questo articolo), pertanto avremo il seguente sistema (2):

(2)

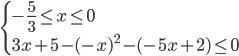
(2)

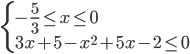
(2)

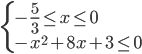
(2)

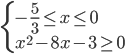
Calcoliamo il Δ/4 della seconda disequazione del sistema:

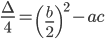
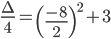
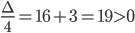
Considerando che il Δ > 0, il coefficiente a > 0; il segno della disequazione è ≥ 0 la disequazione è soddisfatta per valori esterni all’intervallo delle radici che annullano l’equazione associata. Calcoliamo le radici dell’equazione:

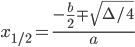
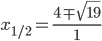
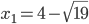
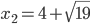
Mettiamo a sistema i risultati delle due disequazioni del sistema (2):

 

 

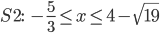
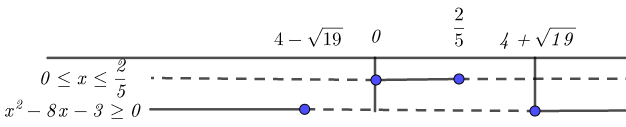
c) Consideriamo ora il terzo intervallo: 0 ≤ x ≤ 2/5 in questo caso il 1° e 2° valore assoluto sono positivi mentre il 3° valore assoluto risulta negativo (fare riferimento sempre al primo grafico inserito in questo articolo), pertanto avremo il seguente sistema (3):

(3)

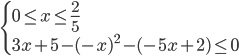
(3)

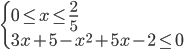
(3)

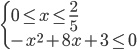
(3)

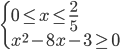
Calcoliamo il Δ/4 della seconda disequazione del sistema:

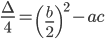
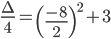
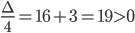
Considerando che il Δ > 0, il coefficiente a > 0; il segno della disequazione è ≥ 0 la disequazione è soddisfatta per valori esterni all’intervallo delle radici che annullano l’equazione associata. Calcoliamo le radici dell’equazione:

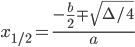
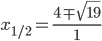
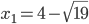
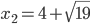
Mettiamo a sistema i risultati delle due disequazioni del sistema (3):

 

 

 

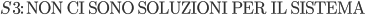
d) Consideriamo ora il quarto e ultimo intervallo: x ≥ 2/5 in questo caso tutti e tre i valori assoluti sono positivi (fare riferimento sempre al primo grafico inserito in questo articolo), pertanto avremo il seguente sistema (4):

(4)

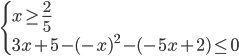
(4)

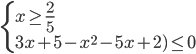
(4)

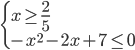
(4)

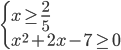
Calcoliamo il Δ/4 della seconda disequazione del sistema:

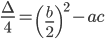
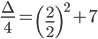
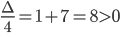
Considerando che il Δ > 0, il coefficiente a > 0; il segno della disequazione è ≥ 0 la disequazione è soddisfatta per valori esterni all’intervallo delle radici che annullano l’equazione associata. Calcoliamo le radici dell’equazione:

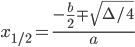
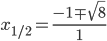
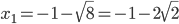
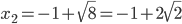
Mettiamo a sistema i risultati delle due disequazioni del sistema (4):

 

 

 

 

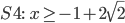
Pertanto la soluzione della nostra disequazione di partenza sarà data dall’unione delle soluzioni dei singoli sistemi:

 

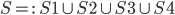
Soluzione della disequazione: