Calcolare la derivata prima della funzione f(x) = e^(x^(-(x^2/2)

Calcoliamo la derivata prima della funzione:

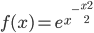
$f(x)=e^{x^{-\frac{x^2}{2}}}$

Dobbiamo applicare la seguente formula:

$\frac{d}{dx}\left[ e^{f(x)} \right]=e^{f(x)}\cdot \frac{d}{dx}\left[ {f(x)} \right]$

Nel nostro caso avremo:

$\frac{d}{dx}\left[ e^{x^{-\frac{x^2}{2}}} \right]=e^{x^{-\frac{x^2}{2}}}\cdot \frac{d}{dx}\left[ x^{-\frac{x^2}{2}} \right]$

Del prodotto, consideriamo ora la funzione da derivare e cioè:

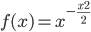
$f(x)= x^{-\frac{x^2}{2}}$

se il 1° membro è uguale al 2° membro lo saranno anche i loro logaritmi naturali:

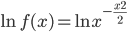
$\ln f(x)= \ln x^{-\frac{x^2}{2}}$

Per la proprietà del logaritmi:

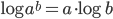
$\log a^b = a\cdot \log b$

possiamo scrivere:

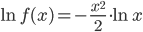
$\ln f(x)= {-\frac{x^2}{2}}\cdot \ln x$

Ora deriviamo ambo i membri:

$\frac{d}{dx}\left[ \ln f(x) \right]= \frac{d}{dx}\left[ -\frac{x^2}{2}\cdot \ln x \right]$

$\frac{d}{dx}\left[ \ln f(x) \right]= -\frac{1}{2}\cdot \frac{d}{dx}\left[ {x^2}\cdot \ln x \right]$

Deriviamo il 1° membro: derivando il logaritmo di una funzione f(x) avremo:

$\frac{d}{dx}\left[ \ln f(x) \right]= \frac{1}{f(x)}\cdot f'(x)$

Deriviamo il 2° membro:

$-\frac{1}{2}\cdot \frac{d}{dx} {x^2}\cdot \ln x=-\frac{1}{2}\cdot \left[ \ln x\cdot \frac{d}{dx}x^2+x^2\cdot\frac{d}{dx}\ln x \right]$

$-\frac{1}{2}\cdot \frac{d}{dx} {x^2}\cdot \ln x=-\frac{1}{2}\cdot \left[ 2x\cdot \ln x+x^2\cdot\frac{1}{x} \right]$

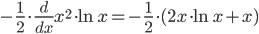
$-\frac{1}{2}\cdot \frac{d}{dx} {x^2}\cdot \ln x=-\frac{1}{2}\cdot (2x\cdot \ln x+x)$

Sostituendo i risultati ottenute dalle derivate del 1° e 2° membro della funzione di partenza, riportata di seguito, avremo:

$\frac{d}{dx}\left[ \ln f(x) \right]= -\frac{1}{2}\cdot \frac{d}{dx}\left[ {x^2}\cdot \ln x \right]$

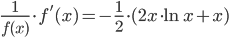
$\frac{1}{f(x)}\cdot f'(x)= -\frac{1}{2}\cdot (2x\cdot \ln x+x)$

Moltiplichiamo ambo i membri per f(x) ottenendo:

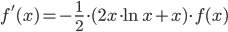
$f'(x)= -\frac{1}{2}\cdot (2x\cdot \ln x+x)\cdot f(x)$

La nostra 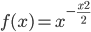$\displaystyle f(x)=x^{-\frac{x^2}{2}}$ per cui sostituendo nella precedente avremo:

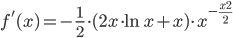
$f'(x)= -\frac{1}{2}\cdot (2x\cdot \ln x+x)\cdot x^{-\frac{x^2}{2}}$

Avendo posto inizialmente:

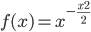
$f(x)= x^{-\frac{x^2}{2}}$

$f'(x)= \frac{d}{dx}\left[x^{-\frac{x^2}{2}}\right]$

da cui:

$f'(x)= \frac{d}{dx}\left[x^{-\frac{x^2}{2}}\right]=-\frac{1}{2}\cdot (2x\cdot \ln x+x)\cdot x^{-\frac{x^2}{2}}$

Ora non ci resta che sostituire quest’ultimo risultato nell’equazione iniziale ottenendo:

$\frac{d}{dx}\left[ e^{x^{-\frac{x^2}{2}}} \right]=e^{x^{-\frac{x^2}{2}}}\cdot \frac{d}{dx}\left[ x^{-\frac{x^2}{2}} \right]$

$\frac{d}{dx}\left[ e^{x^{-\frac{x^2}{2}}} \right]=e^{x^{-\frac{x^2}{2}}}\cdot \left[ -\frac{1}{2}\cdot (2x\cdot \ln x+x)\cdot x^{-\frac{x^2}{2}} \right]$

Italiano – Classe 3^ C primaria

L	M	M	G	V	S	D
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30

SkuolaBlog

BLOG DIDATTICO PERSONALE

Calcolare la derivata prima della funzione f(x) = e^(x^(-(x^2/2)

Lascia un commento Annulla risposta