Equazioni goniometriche elementari del tipo sen x = a

Definizione di equazione goniometrica
un’equazione si dice goniometrica se contiene almeno una funzione goniometrica nell’incognita.

Esempio
è un’equazione goniometrica perchè contiene la funzione seno dell’incognita x.
NON è un’equazione goniometrica perchè non contiene funzioni goniometriche dell’incognita x in quanto è un numero.

Le equazioni elementari devono prima essere ridotte in forma normale in modo da avere una sola funzione al primo membro e un numero reale al secondo membro.

I metodi risolutivi presuppongono:

a) la conoscenza delle definizioni di funzioni goniometriche elementari. E’ conveniente disegnare sempre un grafico della circonferenza goniometrica costruendo gli angoli che soddisfano alla relazione data (soluzione base).
b) la sicura conoscenza dei valori delle funzioni goniometriche elementari di archi noti.
c) un approfondito strudio della periodicità. Ricordiamo infatti che un’equazione elementare, quando non è impossibile ammette infinite soluzioni periodiche, che si ottengono addizionando alla soluzione base  il periodo che vale 2kл per sen e cos e kл per tg e cotg.

Esempio
risolviamo l’equazione

Disegniamo la circonferenza goniometrica nel piano cartesiano, indichiamo gli assi X e Y (in maiuscolo) per non confonderli con l’icognita x dell’equazione e applicando la definizione de seno di un angolo, cerchiamo i punti di ordinata 

Poichè il seno è una funzione periodica di periodo 2л, alle soluzioni e dobbiamo aggiungere sommando quelle dei multipli interi di 2л.
Le soluzioni dell’equazione data sono pertanto:

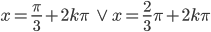
Equazione impossibile

Importante: poichè i valori di senx sono compresi tra -1 e 1, l’equazione sen x = a è impossibile quando a > 1 oppure a < -1
Esempio
l’equazione  non ha soluzioni poichè

In generale l’equazione elementare può essere:
• determinata se -1 ≤ a ≤ 1; una volta trovata una soluzione α, cioè un angolo α tale che sen α = a, le soluzioni dell’equazione sono:
x=α+2kл v x=(л-α)+2kл
• impossibile se a < -1 oppure a > 1
Se per il valore a dell’equazione sen x = a non conosciamo il corrispondente valore dell’angolo del primo o quarto quadrante, possiamo applicare la funzione inversa del seno (x=arcsen a) e calcolare un valore approssimato usando la calcolatrice.

Esempio
  otteniamo:

per trovare il valore approssimato di con la calcolatrice selezioniamo la modalità RAD e dopo aver calcolato , premiamo il tasto, oppure i tasti <INV> e <sin>. In questo modo viene visualizzato il valore della misura in radianti dell’angolo x ossia -1,065435817, che possiamo approssimare alla seconda cifra decimale in -1,07.
Per cui le soluzioni dell’equazione sono;
x≈-1,07+2kл v x≈3,14+1,07+2kл.

Se scegliamo la modalità DEG (gradi), viene visualizzato il valore in gradi sessadecimali. Si ottiene:
-61,04497563≈-61
x≈-61°+k360° v x≈241+k360°.