Esame di Stato liceo scientifico – Anno 2023 – Quesito 6

Determinare i valori dei parametri reali a e b affinché:

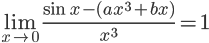
\Large \lim_{x\to 0}\frac{\sin x -(ax^3+bx)}{x^3}=1

Svolgimento:

Calcoliamo il limite per x che tende a zero:

\Large \lim_{x\to 0}\frac{\sin x -(ax^3+bx)}{x^3}=\\ =\frac{\sin 0-(0+0)}{0}=\frac{0}{0}

Abbiamo ottenuto la forma indeterminata 0/0 per cui applichiamo la regola di De l’Hôpital derivando numeratore e denominatore:

\Large \lim_{x\to 0}\frac{\cos x -(3ax^2+b)}{3x^2}=\\ =\frac{\cos 0-(0+b)}{0}=\frac{1-b}{0}

Ora, essendo il denominatore uguale a zero, affinché il risultato del limite sia 0/0 per poter riapplicare di nuovo la regola di De l’Hôpital, deve essere anche il numeratore uguale a zero e cioè:

\Large 1-b=0 \Rightarrow b=1

Sostituendo b=1 nel limite avremo:

\Large \lim_{x\to 0}\frac{\cos x -(3ax^2+1)}{3x^2}

Applichiamo di nuovo la regola di De l’Hôpital derivando numeratore e denominatore:

\Large \lim_{x\to 0}\frac{-\sin x -(6ax)}{6x}=\\ =\frac{-\sin 0 -(0)}{0}=\frac{0}{0}

Avendo ottenuto di nuovo una forma indeterminata 0/0 riapplichiamo la regola di De l’Hôpital:

\Large \lim_{x\to 0}\frac{-\cos x -(6a)}{6}=\\ =\frac{-\cos 0 -(6a)}{6}=\frac{-1 -6a}{6}

Poniamo il risultato del limite ottenuto = 1 :

\Large \frac{-1 -6a}{6}=1

\Large -1 -6a=6 \Rightarrow -6a=7 \Rightarrow a=-\frac{7}{6}

Giugno 23, 2023 , Analisi, Matematica No Comments »


Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *

error: Contenuto protetto !!

Apri un sito e guadagna con Altervista - Disclaimer - Segnala abuso - Privacy Policy - Personalizza tracciamento pubblicitario