[Geometria] Criteri di congruenza dei triangoli – Esercizi
Esercizio 1
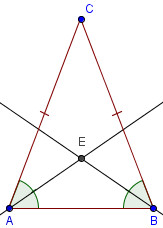Sia ABC un triangolo isoscele di base AB. Si conducano le bisettrici degli angoli alla base e sia E il loro punto d’incontro. Dimostrare che il triangolo ABE è isoscele.
Allora essendo ABC isoscele avremo che saranno congruenti i lati AC=BC e gli angoli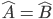 
. Disegnamo ora le bisettrice degli angoli 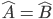che essendo congruenti daranno origine a quattro angoli congruenti: 
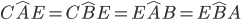per cui possiamo affermare che il triangolo ABE è isoscele avendo gli angoli alla base 
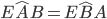pertanto saranno congruenti anche i lati AE=BE.
Esercizio 2
Sui lati congruenti del triangolo isoscele ABC, di vertice C, disegna due segmenti congruenti CE e CF. Congiungi E con B, poi A con F; indica con D il loro punto d’intersezione. Dimostra che anche il triangolo ABD è isoscele.
Allora essendo per ipotesi ABC isoscele avremo che i lati AC=BC e gli e gli angoli 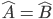. Consideriamo ora i due triangoli ACF e BCE questi due triangoli hanno AC=BC per ipotesi CE=CF per costruzione e l’angolo 
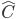in comune, risultano uguali per il 1° criterio di congruenza dei triangoli pertanto avranno congruenti tutti gli altri elementi: i lati AF=BE e gli angoli 
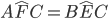e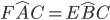 
.
Consideriamo ora i due triangoli ADE e BDF i quali hanno il lato AE=BF (infatti AC=BC per ipotesi e CE=CF per costruzione quindi AE=BF per differenza di lati uguali: AC-CE=BC-CF), hanno uguali gli angoli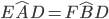 
(lo abbiamo dimostrato al punto precedente) e anche gli angoli 
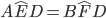in quanto supplementari di angoli uguali (sono supplementari di 
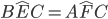) pertanto i due triangoli avendo un lato e i due angoli ad esso adiacenti congruenti risultano congruenti per il 2° criterio; da ciò ne deriva che sono congruenti anche tutti gli altri elementi in particolare AD=BD.
Pertanto possiamo affermare che il triangolo ABD è isoscele su base AB avendo i lati obliqui AD=BD.
Esercizio 3
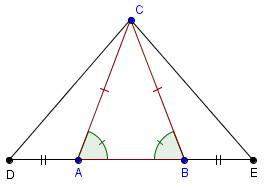Sia ABC un triangolo isoscele di vertice C; si prendano sui prolungamenti di AB due punti D ed E tali che AD = BE. Si dimostri che ADC = BEC e AEC = BDC.
- Allora esaminiamo i due triangoli ADC e BEC questi hanno AC=BC per costruzione, AD=BE per costruzione e gli angoli
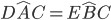perchè sono complementari di angoli uguali (degli angoli alla base del triangolo isoscele ABC). Pertanto avendo due lati uguali e l’angolo tra essi compreso uguali risultano congruenti per il 1° criterio di congruenza dei triangoli; quindi avranno congruenti tutti gli altri elementi: l’angolo 
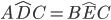; l’angolo 
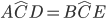ed il lato DC=EC. - Consideriamo ora i triangoli AEC e BDC si può notare che, per dimostrare la loro congruenza possiamo procedere in tre modi:
- il lato AE=BD per costruzione (sono ambedue somma di lati uguali: AE=AB+BE e BD=BA+AD per cui AB è in comune e AD=BE per costruzione); il lato AC=BC per costruzione (sono lati obliqui del triangolo isoscele ABC) e l’angolo
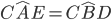per costruzione (sono gli angoli alla base del triangolo isoscele ABC); pertanto i due triangoli avendo due lati e l’angolo tra essi compreso uguale risultano congruenti per il 1° criterio.
- il lato AE=BD per costruzione (sono ambedue somma di lati uguali: AE=AB+BE e BD=BA+AD per cui AB è in comune e AD=BE per costruzione); l’angolo 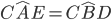per costruzione (sono gli angoli alla base del triangolo isoscele ABC) e
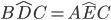(lo abbiamo dimostrato al punto 1. sono angoli uguali dei due triangoli congruenti ADC e BEC); pertanto i due triangoli avendo un lato e i due angoli ad esso adiacenti uguali risultano congruenti per il 2° criterio.
- dopo aver dimostrato la congruenza dei triangoli ADC e BEC avremo:
– l’angolo
perchè somma di angoli uguali;
– DC = EC come dimostrato nella congruenza dei triangoli ADC e BEC;
– AC = BC per ipotesi
I due triangoli avendo due lati e l’angolo tra essi compreso uguale risultano congruenti per il 1° criterio. (ringraziamo Laura per questa ulteriore dimostrazione).
Esercizio 4
Sui due lati obliqui de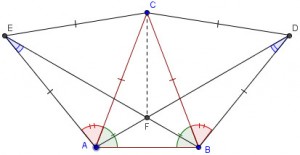
l triangolo isoscele ABC, di base AB, disegna esternamente al triangolo, i triangoli equilateri BCD e ACE. Congiungi A con D e B con E, indica con F il punto di intersezione dei segmenti ottenuti. Dimostra che:
a) AD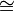 
BE (AD congruente a BE)
b) CF è bisettrice dell’angolo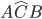 
- Sappiamo allora che il triangolo ABC è isoscele e quindi: AC
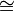BC e gli angoli alla base sono uguali cioè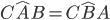 
- Sappiamo inoltre che i due triangoli BDC e AEC sono equilateri per costruzione e quindi avranno i tre lati uguali (che sono uguali a due lati obliqui del triangolo isoscele) per cui: AE=EC=AC=BC=CD=BD e anche gli angoli sono tutti uguali
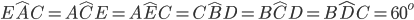
- Consideriamo ora i due triangoli ABE e BAD che hanno il lato AE 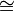BD per costruzione; il lato AB in comune e l’angolo
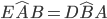perchè somma di angoli uguali per cui i due triangoli risultano congruenti per il 1° criterio e pertanto anche il lato AD 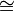BE e gli angoli 
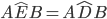e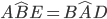 
. Da quest’ultima affermazione ricaviamo che il triangolo AFB su base AB ha gli angoli alla base uguali quindi è isoscele e pertanto sono congruenti i lati obliqui: FA = FB. - Consideriamo ora i due triangoli FCA ed FCB che hanno i lati CA=CB per costruzione, i lati FA = FB (lo abbiamo dimostrato al punto precedente) ed il terzo lato CF in comune, pertanto risultano congruenti per il 3° criterio. Da ciò ricaviamo che sono uguali rispettivamente i tre angoli in particolare
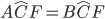per cui possiamo affermare che il segmento CF è la bisettrice dell’l’angolo 
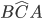in quanto divide tale angolo in due parti uguali.
L’ esercizio 4 ha la seconda tesi sbagliata, è CF la bisettrice dell’angolo ACB
Riccardo, grazie per la precisazione; è vero ho preso una svista scrivendo la bisettrice dell’angolo. Adesso ho sistemato tutto (almeno spero).
mi serve un aiuto in un problema..
se ABC è un triangolo isoscele di base AB e se M e N sono due punti appartenenti rispettivamente ai lati AC e BC tali che CM=CN allora AN=BM. se ,inoltre, F denota il punto D intersezione di AN con BM allora anche il triangolo ABF è isoscele.
* il punto di intersezione (non D)
Eleonora,
guarda che il tuo esercizio è uguale all’Esercizio n.2, quindi è già domostrato.
Skuolablog.
La tesi sostenuta all’esercizio 1 non richiede affatto alcuna conoscenza sui criteri di congruenza dei triangoli.
Sarebbe ben diversa la cosa se, con quelle ipotesi, si dovesse dimostrare, per es., la congruenza dei segmenti staccati dalle due bisettrici sui due lati congruenti del triangolo (isoscele) in oggetto.
Ciao Rino,
come ho già più volte premesso, non sono un professore di matematica, ma attraverso il BLOG cerco di aiutare i miei figli nello studio. Premesso ciò, ti dico che hai perfettamente ragione, ma siccome l’esercizio era riportato tra quelli risolvibili con i criteri di congruenza dei triangoli l’ho lasciato (forse a torto) in questa pagina di esercizi.
in un triangolo ABC AB=A’B’ BC=B’C’ e l’angolo compreso fra essi(alfa) è congruente all’altro(alfa’)con quale criterio si può dimostrare che ABC=A’B’C’?
Con il secondo criterio di similitudine. Se vuoi ripassare la teoria guarda il seguente link:
http://www.ripmat.it/mate/f/fp/fpfc.html
Skuolablog
ho un problema:
Sia ABC un triangolo, in cui AC<AB. Sulla bisettrice dell' angolo BAC, cosidera il punto D tale che AD sia congruente a AC e il punto E tale che AE sia congruente a AB.
Dimostra che i segmenti AD e DE sono congruenti.
Considera un punto P sul segmento BD e dimostra che PED è congruente a PAD.
Salve,
in riferimento all’esercizio numero 3.
Dopo aver dimostrato la congruenza dei triangoli ADC e BEC, la congruenza dei triangoli AEC e BDC l’ho dimostrata nella seguente maniera:
-Angolo C in comune
-DC= EC perché appena dimostrato nella precedente dimostrazione riguardante ADC e BEC
-AC=BC per ipotesi
I due triangoli sono congruenti per il primo criterio. La mia dimostrazione è errata oppure ci sono più metodi per arrivare alla stessa conclusione?
Laura grazie per averci scritto, la tua dimostrazione va benissimo tanto è vero che l’ho inserita nel testo dell’esercizio.
Un saluto.
Skuolablog.
Buongiorno SkuolaBlog. Avrei una domanda: nell’esercizio 2 nel procedimento dei due triangoli, gli angoli ADE e BDF possono essere congruenti perché opposti al vertice?
Carissimo Andrea, naturalmente si.
Gli angoli opposti al vertice sono sempre uguali quindi come hai indicato ADE e BDF sono sicuramente uguali in quanto opposti al vertice.