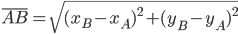Scrivi l’equazione della tangente alla circonferenza di equazione x²+y²+9y-9=0

Es. di Geometria Analitica n.385 pag.413

[su_note note_color=”#faff66″ text_color=”#1416bc”]Scrivi l’equazione della tangente alla circonferenza di equazione x²+y²+9y-9=0 condotte dal punto (3/2; 3), e verifica che sono perpendicolari. Determina poi le coordinate dei punti di tangenza e la misura della corda che li congiunge.[/su_note]
—————–

Scriviamo l’equazione di una retta passante per il punto dato e di coefficiente angolare m non noto:

y-3=m(x-3/2)

y-3=mx-3/2m

mx-y-3/2m+3=0 moltiplichiamo ambo i membri per 2

2mx-2y-3m+6=0

Partendo dall’equazione della circonferenza x²+y²+9y-9=0 calcoliamo le coordinate del centro della circonferenza:

$C\left(-\frac{a}{2},\;-\frac{b}{2} \right )\Rightarrow C\left(0,\;-\frac{9}{2} \right )$

Calcoliamo ora la lunghezza del raggio:

$r=\sqrt{\frac{a^2}{4} + \frac{a^2}{4}-c}$

$r=\sqrt{0 + \frac{81}{4}+9}$

$r=\sqrt{\frac{117}{4}} = \frac{3}{2}\sqrt{13}$

A questo punto possiamo applicare la formula per calcolare la distanza di un punto da una retta dove il punto è il centro della circonferenza C(0, -9/2) e la retta è 2mx-2y-3m+6=0

$d=\frac{|a\cdot x_0+b\cdot y_0+c|}{\sqrt{a^2+b^2}}$

dove a, b, c sono i coefficienti dell’equazione della retta e xo, yo sono le coordinate del punto.

$d=\frac{\left |0+(-2)\cdot\left(-\frac{9}{2} \right )-3m+6 \right|}{\sqrt{(2m)^2+(-2)^2}}$

$d=\frac{\left |9-3m+6 \right|}{\sqrt{4m^2+4}}$

$d=\frac{\left |15 - 3m \right|}{2\sqrt{m^2+1}}$

Ora imponiamo che questa distanza sia uguale al raggio e calcoliamo il coefficiente angolare m:

$\frac{\left |15-3m \right|}{2\sqrt{m^2+1}}=\frac{3}{2}\sqrt{13}$

Moltiplichiamo ambo i membri per $2\sqrt{m^2+1}$ ottenendo:

$\left |15-3m \right|=\frac{3}{2}\sqrt{13}\cdot 2\sqrt{m^2+1}$

$\left |15-3m \right| = 3\sqrt{13m^2+13}$

Eleviamo al quadrato ambo i membri togliendo anche il valore assoluto:

$(15-3m)^2=(3\sqrt{13m^2+13})^2$

$225+9m^2-90m=117m^2+117$

$117m^2-9m^2+90m+117-225=0$

$108m^2+90m-108=0$

dividiamo ambo i membri per 18:

$6m^2+5m-6=0$

Calcoliamo il Delta:

$\Delta=b^2-4ac=225+144=169$

$m_{1/2}=\frac{-b \mp \sqrt{\Delta}}{2a}$

$m_{1/2}=\frac{-5\mp \sqrt{169}}{12}$

$m_{1}=\frac{-5-13}{12}=-\frac{18}{12}=-\frac{3}{2}$

$m_{1}=\frac{-5+13}{12}=\frac{8}{12}=-\frac{2}{3}$

Sostituendo nell’equazione della retta y-3=m(x-3/2) il coefficiente angolare m=-3/2 avremo:

$y-3=-\frac{3}{2} \left( x-\frac{3}{2} \right )$

$y-3=-\frac{3}{2}x+\frac{9}{4}$

$y=-\frac{3}{2}x+\frac{9}{4}+3$

$y = -\frac{3}{2}x + \frac{21}{4}$

Sostituendo nell’equazione della retta y-3=m(x-3/2) il coefficiente angolare m=2/3 avremo:

$y-3 = \frac{2}{3} \left( x-\frac{3}{2} \right )$

$y-3=\frac{2}{3}x-1$

$y=\frac{2}{3}x-1+3$

$y=\frac{2}{3}x+2$

Osservando le equazioni delle due rette notiamo che il coefficiente angolare della prima retta è m=–3/2, mentre il coefficiente della seconda retta è m’=2/3, per cui essendo i due coefficienti angolari uno l’antireciproco dell’altro (m=–1/m’)possiamo concludere che le due rette sono tra loro perpendicolari (o normali).