Calcolo distanza AB e punto medio.
Considera i punti A(a+2; 1) e B(3; b-1), con a e b numeri reali. Determina a e b in modo che la distanza AB sia uguale a 1 e che il punto medio M del segmento AB abbia ordinata 
. Trova poi i punti C sull’asse y la cui distanza da A è 
Per la soluzione del problema calcoliamo la distanza tra i due punti AB ottenendo una equazione nelle incognite a e b e la poniamo = 1; calcoliamo poi il punto medio M di AB (ci basta solo l’ordinata yB) e la poniamo 
; a questo punto si tratta di risolvere un sistema di equazioni in due incognite a e b.
Dalla formula per il calcolo della distanza fra due punti avremo:
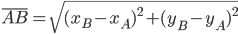
Dovendo essere AB = 1 avremo:
Calcolo adesso l’ordinata del punto medio di AB
Dovendo essere il punto medio situato sulla retta 
la sua ordinata sarà sempre 
per cui possiamo scrivere:
Mettiamo ora a sistema le due equazioni ottenute:
Calcoliamo b dalla 2^ equazione del sistema poi eleviamo al quadrato ambo i membri della 1^ equazione, sostituiamo b e calcoliamo a:
moltiplichiamo ambo i membri per 2:
eleviamo ambo i membri al quadrato:
sostituiamo b=1:
calcolo il Delta quarti: 
quindi a=1 e b=1 per cui sostutuendo avremo:
A(a+2; 1) → A(3; 1)
B(3; b-1) → B(3; 0)
A questo punto dobbiamo trovare i punti C che stanno sull’asse y e hanno coordinate C(0; y).
Deve quindi essere 
ovvero 
abbiamo cioè utilizzato la formula per il calcolo della distanza AC ponendo il risultato 
elevando al quadrato ambo i membri:
dove A(3; 1) e C(0; y) per cui avremo:
L’equazione precedente rappresenta un trinomio del tipo 
dove S e P rappresentano rispettivamente la somma ed il prodotto delle due soluzioni y1 e y2 e questi due numeri che ci danno come somma S = –2 e come prodotto P = –80 sono +8 e –10 infatti S = +8 –10 = –2 mentre P = 8(–10) = –80 per cui l’equazione precedente può essere scritta come il seguente prodotto:
per cui avremo:
C1(0; -8)
C2(0; 10)
Nota: gli esercizi sono tratti dal libro Matematica Blu 2.0 vol 3 – Zanichelli Editore