[Fisica] In laboratorio hai eseguito l’esperienza Equilibrio di un corpo su un piano inclinato
n. 2 pag. 209
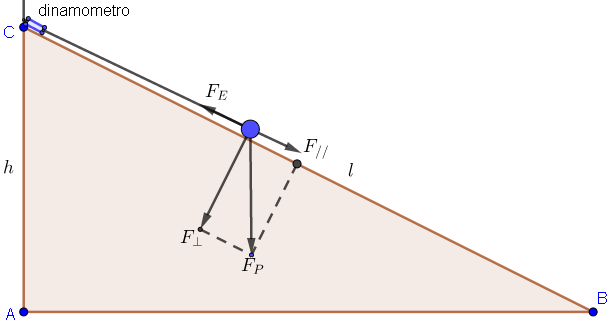
[su_note note_color=”#faff66″ text_color=”#1416bc”]In laboratorio hai eseguito l’esperienza “Equilibrio di un corpo su un piano inclinato”. Hai posizionato sul piano un carrellino di massa (500 ± 1) g e lo hai collegato tramite un filo inestensibile e di massa trascurabile a un dinamometro, agganciato all’estremità superiore del piano. La situazione è rappresentata in figura. Con un metro hai misurato l’altezza e la lunghezza del piano, mentre hai letto direttamente l’intensità della forza equilibrante sulla scala del dinamometro. Le misure sono riportate in tabella:
| ALTEZZA PIANO INCLINATO | LUNGHEZZA PIANO INCLINATO | FORZA EQUILIBRANTE |
|---|---|---|
| (30,0 ± 0,1) cm | (60,0 ± 0,1) cm | (2,5 ± 0,1) N |
Considera il carrello come puntiforme.
a. Disegna le forze agenti sul corpo.
b. In base alle considerazioni di natura geometrica, stabilisci quanto vale l’angolo di inclinazione del piano.
c. Calcola il modulo del vettore componente della forza-peso parallelo all’ipotenusa del piano inclinato (F//) con l’incertezza. Giudica se il valore calcolato di F// è in accordo con il valore misurato della forza equilibrante.
d. La casa costruttrice fornisce un valore nominale di 100 N/m per la costante elastica della molla del dinamometro. Calcola a quanto corrisponde l’allungamento della molla nelle condizioni sperimentali indicate nella tabella.[/su_note]
a. Disegno
b. Calcoliamo ora l’angolo di inclinazione del piano:
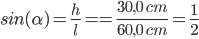
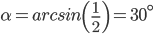
Considerazioni di natura geometrica:
Il piano inclinato è rappresentato da un triangolo rettangolo ABC che ha il cateto minore (AC=30,0 cm) che è la metà dell’ipotenusa (BC=60,0 cm); da questo ricaviamo che si tratta di un triangolo rettangolo di angoli 30°, 60° e 90° essendo la metà di un triangolo equilatero. L’angolo di inclinazione del piano essendo opposto al cateto minore vale 30°.
c. Calcoliamo F// (modulo del vettore componente della forza-peso che è parallelo all’ipotenusa) con la relativa incertezza:
m = (500 ± 1) g = (0,5 ± 0,001) kg
Fp = m•g = (0,5 ± 0,001) kg • 9,8 N/kg = (4,9 ± 0,01) N
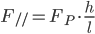
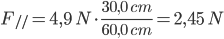
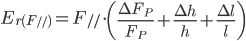
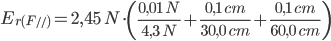
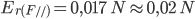
Ora possiamo scrivere F// con la relativa incertezza:
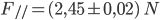
Considerazioni:
Considerando i dati del problema e il grafico rappresentato in figura, possiamo affermare che gli obiettivi sono stati raggiunti in quanto attraverso i calcoli effettuati il risultato della forza parallela risulta quasi uguale al valore misurato della forza equilibrante. La piccola differenza tra le due misure, che comunque risulta accettabile, è dovuta molto probabilmente a errori casuali come l’errore di parallasse, l’errore di lettura poco precisa sul metro o sul dinamometro utilizzato e anche alla leggera usura nel tempo della molla del dinamometro.
d. Calcoliamo l’allungamento della molla sapendo che k = 100 N/m
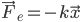
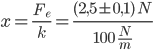
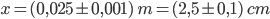
[su_quote]Nota: gli esercizi sono tratti dal libro di testo “Dalla mela di Newton al bosone di Higgs PLUS” Esercizi STATICA parte 5 L’EQUILIBRIO DEI SOLIDI pag. 209.[/su_quote]